NTRANDTRUNCNORM

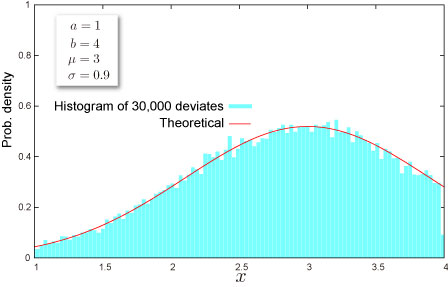
切断正規分布に従う疑似乱数を返します。乱数は超長周期 ($2^{19937}-1$)、 かつ高次元均等性（623次元）を備えたMersenne Twister アルゴリズム を基に生成されます。

書式

NTRANDTRUNCNORM(
    Size,
    Min,
    Max,
    Mu,
    Sigma,
    Algorithm,
    Random seed1,
    Random seed2
)

引数

• Size乱数の個数を指定します（正の整数）。
• Min 分布の下限値 $a$ を指定します。
• Max 分布の上限値 $b$ を指定します。
• Mu 分布のパラメータ $\mu$ を指定します。
• Sigma 分布のパラメータ $\sigma(>0)$ を指定します。
• Algorithm 一様乱数を生成するアルゴリズムを下記の3つから選択します。この引数は省略することができます。
  • 0: Mersenne Twister(2002)
  • 1: Mersenne Twister(1998)
  • 2: Numerical Recipes ran2()
• Random seed1 第1乱数シードを指定します。この引数は省略することが出来ます。
• Random seed2 第2乱数シードを指定します。この引数は省略することが出来ます。

解説

• パラメータ $a$ と $b$ は $a < b$ である必要があります。

• 乱数$x$ は、$(0,1)$ の一様乱数$U$から、

  $$x=\sigma\Phi^{-1}\left[\Delta U +\Phi(A)\right]+\mu$$

  として計算されます（逆関数法）。ここで、$\Phi(\cdot)$ は標準正規分布の累積分布関数で、

  $$\Delta=\Phi(B)-\Phi(A)$$ $$A=\frac{a-\mu}{\sigma},B=\frac{b-\mu}{\sigma}$$

  です。

使用例

• 使用例を新規のワークシートにコピーすると、計算結果を確認できます。

その方法は？

1. 新しいブックまたはワークシートを作成します。

2. ヘルプ トピックにある使用例を選択します（行番号および列番号を除く）。

   

   ヘルプから使用例を選択する

3. Ctrl キーを押しながら C キーを押します。

4. ワークシートのセル A1 を選択し、Ctrl キーを押しながら V キーを押します。

5. 計算結果と結果を返す数式の表示を切り替えるには、Ctrl キーを押しながら ` (アクサン グラーブ) キーを押すか、または [ツール] メニューの [ワークシート分析] をポイントし、[ワークシート分析モード] をクリックします。

	A	B
1	データ	説明
2	1	分布の下限
3	4	分布の上限
4	3	パラメータ Mu の値
5	0.9	パラメータ Sigma の値
6	数式	説明（計算結果）
7	=NTRANDTRUNCNORM(100,A2,A3,A4,A5,0)	100個の切断正規乱数を Mersenne Twister アルゴリズムで生成します。

メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A7:A106 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

• サンプル Excel シートをダウンロード

参照

• NTTRUNCNORMDIST
• NTTRUNCNORMINV
• NTTRUNCNORMKURT
• NTTRUNCNORMMEAN
• NTTRUNCNORMMOM
• NTTRUNCNORMPARAM
• NTTRUNCNORMSKEW
• NTTRUNCNORMSTDEV
• 切断正規分布
• 乱数アルゴリズムの選択
• どうして複数のセルに数式をコピーすると全部同じ結果になるの？