正規分布（単変量）(Normal distribution)

あの鐘を鳴らすのは正規分布

ベル=カーブ

**正規分布（英名 "Normal distribution"）**は確率・統計で間違いなく最も重要な分布です。実際これを知らないと何もできない程！19世紀最大の科学者カール・フリードリヒ・ガウスが導入したことから、ガウス分布とも呼ばれています（彼の故郷、ドイツの旧10マルク紙幣にはガウスの自身と正規分布の形が描かれていました）。

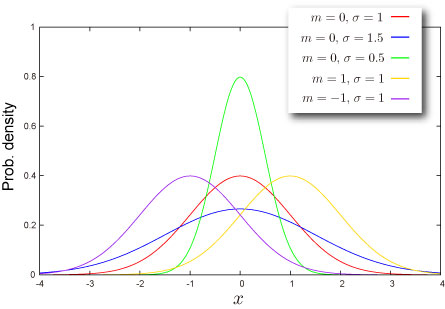
先ずは正規分布の確率密度関数の形を見てみましょう。

• 左右対称
• 中心部分が一番高く、中心から離れれば離れるほど急速に減少していく
• （見ただけでは分からないけど）実はグラフは永遠に伸びていて、水平軸に接することはない。

均整のとれたこの形は古き良き時代の鐘を想起させることから「ベル＝カーブ」という愛称も持っています。

分布の特徴

正規分布の形状はなんとたった2つの情報で決まってしまいます。

• 分布の位置を決める 平均。通常 $m$ と表記されることが多い。
• 分布の広がりを決める 標準偏差。通常 $\sigma$（ギリシャ文字の"シグマ"）と表記されることが多い。

数式を少々（我慢我慢）

とにかく重要でどこにでも顔を出す分布なので、ここはひとつ数式を見てみましょう。他でもしょっちゅう出てくるものばかりで、きっと試験にも出ます。どうにか我慢してお付き合いください。

• 確率密度関数
  上でみたベル=カーブを描き出す関数は、

  $$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{(x-m)^2}{2\sigma^2}\right]$$

  と与えられます。ここで$m=0$、$\sigma=1$としてみると（つまり標準正規分布）、

  $$f(x)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right)$$

  となります。この関数は $\phi(x)$ （ギリシャ文字の "ファイ" の小文字）と表記されます。この $\phi(\cdot)$ を使うと、標準じゃない正規分布は、

  $$f(x)=\frac{1}{\sigma}\phi\left(\frac{x-m}{\sigma}\right)$$

  となります。

• 累積分布関数
  累積分布関数は確率密度関数を積分したもの！としかいいようがありません。

  $$F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{x}\exp\left[-\frac{(t-m)^2}{2\sigma^2}\right]\text{d}t$$

  これも標準正規分布の場合には特別な表記が与えられています。

  $$\Phi(x)=\int_{-\infty}^{x}\phi(t)\text{d}t$$

  $\Phi$ はギリシャ文字の"ファイ"の大文字です。この $\Phi(\cdot)$ を使うと標準じゃない正規分布は、

  $$F(x)=\Phi\left(\frac{x-m}{\sigma}\right)$$

  となります。

その他のトピック

• 左右対称ということから、この分布の歪度（ゆがみ）は 0
• 正規分布の尖度（とがり具合）を 0 として、この分布より裾が厚い分布（尖度が正）を "Leptokurtic"な分布、裾が薄い分布（尖度が負）を "Platykurtic"な分布と呼ぶ
• 多数の分布の極限が正規分布になるということと、多数の不確定要素の積み重ねが正規分布を生み出す（中心極限定理）という事実によって、この分布はどこにでも顔を出す。

分布の形状

基本情報

• 無限区間 $(-\infty,+\infty)$ で定義された連続分布です。

確率

• 累積分布関数

  $$F(x)=\frac{1}{\sigma}\int_{-\infty}^{x}\phi\left(\frac{t-m}{\sigma}\right)\text{d}t$$

  ここで $\phi(\cdot)$ は標準正規分布の確率密度関数です。

• 確率密度関数

  $$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{(x-m)^2}{2\sigma^2}\right]$$

• Excel での累積分布関数 (c.d.f.) と 確率密度関数 (p.d.f.)の求め方

	A	B
1	データ	説明
2	0.5	対象となる値
3	8	分布のパラメータ M の値
4	2	分布のパラメータ Sigma の値
5	数式	説明（計算結果）
6	=NTNORMDIST((A2-A3)/A4,TRUE)	上のデータに対する累積分布関数の値
7	=NTNORMDIST((A2-A3)/A4,FALSE)	上のデータに対する確率密度関数の値

• 関連 NtRand 関数 : NTNORMDIST
• 第2引数が TRUE の場合、NtRand 関数 NTNORMDIST は Excel 関数 NORMSDIST と同等です。

分位点

• 累積確率関数の逆関数

  $$F^{-1}(P)=\sigma\Phi^{-1}(P)+m$$

  ここで $\Phi(\cdot)$ は標準正規分布の累積分布関数です。

• Excel での分位点の求め方

	A	B
1	データ	説明
2	0.7	この分布の確率
3	1.7	分布のパラメータ M の値
4	0.9	分布のパラメータ Sigma の値
5	数式	説明（計算結果）
6	=A4*NORMSINV(A2)+A3	上のデータに対する累積分布関数の逆関数の値

• NORMSINV は Excel 関数です。

分布の特徴

平均 -- 分布の"中心"はどこ？ (定義)

• 分布の平均は $m$ と与えられます。

標準偏差 -- 分布はどのくらい広がっているか（定義）

• 分布の標準偏差は $\sigma$ と与えられます。

歪度 -- 分布はどちらに偏っているか(定義)

• 分布の歪度は $0$ です。

尖度 -- 尖っているか丸まっているか (定義)

• 分布の尖度は $0$ です。

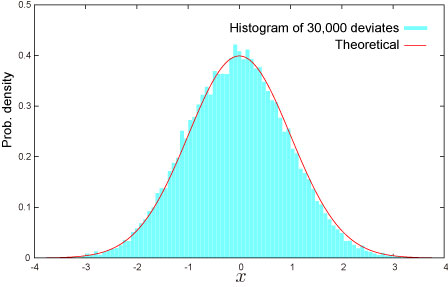
乱数

Excel での乱数生成法

	A	B
1	データ	説明
2	0.5	分布のパラメータ M の値
3	0.5	分布のパラメータ Sigma の値
4	数式	説明（計算結果）
5	=A3*NTRANDNORM(100)+A2	100個の正規乱数を Mersenne Twister アルゴリズムで生成します。

メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A5:A104 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

関連 NtRand 関数

• Mersenne Twiseter 法による乱数生成 : NTRANDNORM

参照

• Wolfram Mathworld -- Normal Distribution
• Wikipedia -- Normal distribution
• Statistics Online Computational Resource