Normal Distribution (Single variable)

Where do you meet this distribution?

• Standard score
• Finance, Economics : changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal
• Average of stochastic variables : Central Limit Theorem
• Statistical mechanics : Velocities of the molecules in the ideal gas
• Quantum physics : Probability density function of a ground state in a quantum harmonic oscillator
• Error analysis

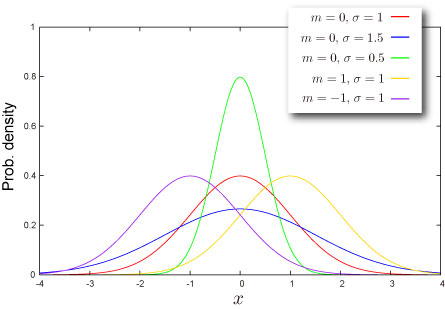
Shape of Distribution

Basic Properties

• Two parameters $m, \sigma$ are required.

$$\sigma>0$$

These parameters are Mean and Standard Deviation of the distribution respectively.

• Continuous distribution defined on entire range
• This distribution is always symmetric.

Probability

• Cumulative distribution function

$$F(x)=\int_{-\infty}^{x}\phi\left(\frac{t-m}{\sigma}\right)\text{d}t$$

where $\phi(\cdot)$ is Probability density function of standard normal distribution.

• Probability density function

$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{(x-m)^2}{2\sigma^2}\right]$$

• How to compute these on Excel.

	A	B
1	Data	Description
2	0.5	Value for which you want the distribution
3	8	Value of parameter M
4	2	Value of parameter Sigma
5	Formula	Description (Result)
6	=NTNORMDIST((A2-A3)/A4,TRUE)	Cumulative distribution function for the terms above
7	=NTNORMDIST((A2-A3)/A4,FALSE)	Probability density function for the terms above

• Function reference : NTNORMDIST
• NtRand Function NTNORMDIST is same as excel function NORMSDIST when 2nd. argument=TRUE.

Quantile

• Inverse function of cumulative distribution function

  $$F^{-1}(P)=\sigma\Phi^{-1}(P)+m$$

  where $\Phi(\cdot)$ is cumulative distribution function of standard normal distribution.

• NORMSINV is an excel function

• How to compute this on Excel.

	A	B
1	Data	Description
2	0.7	Probability associated with the distribution
3	1.7	Value of parameter M
4	0.9	Value of parameter Sigma
5	Formula	Description (Result)
6	=A4*NORMSINV(A2)+A3	Inverse of the cumulative distribution function for the terms above

Characteristics

Mean -- Where is the "center" of the distribution? (Definition)

• Mean of the distribution is given as $m$.

Standard Deviation -- How wide does the distribution spread? (Definition)

• Standard deviation of the distribution is given as $\sigma$.

Skewness -- Which side is the distribution distorted into? (Definition)

• Skewness of the distribution is given as $0$.

Kurtosis -- Sharp or Dull, consequently Fat Tail or Thin Tail (Definition)

• Kurtosis of the distribution is given as $0$.

Random Numbers

• How to generate random numbers on Excel.

	A	B
1	Data	Description
2	0.5	Value of parameter M
3	0.5	Value of parameter Sigma
4	Formula	Description (Result)
5	=A3*NTRANDNORM(100)+A2	100 Normal deviates based on Mersenne-Twister algorithm for which the parameters above

Note The formula in the example must be entered as an array formula. After copying the example to a blank worksheet, select the range A5:A104 starting with the formula cell. Press F2, and then press CTRL+SHIFT+ENTER.

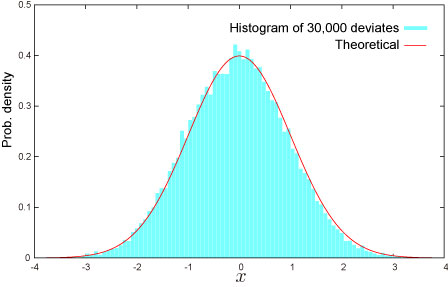
NtRand Functions

• Generating random numbers based on Mersenne Twister algorithm: NTRANDNORM

Reference

• Wolfram Mathworld -- Normal Distribution
• Wikipedia -- Normal distribution
• Statistics Online Computational Resource