指数分布(Exponential distribtuion)
雑踏の中を歩く指数分布
都会の雑踏を歩いていると、1メートル進んでは人にぶつかり、3メートル進んでは人にぶつかり、となかなかスムーズに歩けないですよね(え、私だけ?)。
直感的に考えて
- 長い距離ぶつからずに歩ける確率は少ない
- 人がたくさんいると短い距離歩くだけでぶつかる
というのは理解できると思います。では、人とぶつかるタイミングはどういった分布に従うのでしょうか?
まず、雑踏をそのままモデル化するのは難しそうです。そこで簡単なモデルを考えることにします。
歩いている人間は複雑すぎるので、1本道上で人はみんな止まっていると仮定します。ある人の場所から歩いて、次の人までぶつからずに歩く。 このモデルで人と人との間隔の分布を調べてみましょう。
このモデルでもいきなり一般的な話をすると難しいから、更に簡単な状況からスタートすることにしますね。
さて、100メートルの道があります。自分の今いる場所から1メートル先の地点、そこから100個のベンチが1メートル間隔で並んでいます。そこに20人の人が座ることとします。ただし以下の条件の制約があります。
- 1つのベンチには1人しか座れない。
- 座り心地の良いベンチがあるとか、日陰と日なたにあるベンチがあるとか、嫌いな奴から離れて座りたいとか、どこかのベンチにモデル級の美女が座っていて、その周辺に何人か集まって座るとか、そういったことはありません。つまりどのベンチに座るかは「同様に確からしい」のです。
図の赤丸が人がいるベンチ、白抜きの丸が空のベンチです。
以上から、どのベンチでも人がいる確率は同様に確からしく となります。
では勇気を持って歩き出してください。
- 隣のベンチに人はいなかった
- その隣のベンチにも人はいなかった
- その隣のベンチには人がいた
この状況、つまり2メートル人と出会わなかった確率を求めてみましょう。
先ず隣のベンチに人がいない確率は
となります(ベンチに人がいる確率はであることを思いだして)。 その隣にも人がいないので、ここまでの確率は
となります。そして次に人が出現。結局2メートル人と出会わない確率は
です。
ここまで来れば、あるベンチから右側に個分のベンチに人がいなくて、その次に人がいる(つまりメートル人と出会わない)確率は、
であることが分かります。
では次ステップに移りましょう。ベンチの数を倍にして50センチ間隔に配置してみます。ベンチの数は倍の200個、人の数は変わらず20人になるので、ベンチに人がいる確率は 0.1 となりますね。
こで個のベンチを挟んで、次のベンチに人がいる(つまりメートル人と出会わない)確率は、
となります。
さらにベンチの間隔を半分にします。ベンチが400個、人は20人。個のベンチを挟んで、次に人がいる(つまりメートル人と出会わない)確率は、
となります。
ここまでの様子を図に示してみます(の場合)。
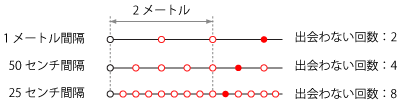
もうここまでくれば、一般化は簡単ですね。
ベンチの間隔をとしましょう。
メートル人と会わない確率は、
となります(ちなみにこの分布は幾何分布と呼ばれます)。一方で隣の人までの距離がメートル以下である確率を と書くと、隣の人ととの距離が より離れていて メートル以下である確率が
であることは分かるでしょうか?
結局、
が得られることとなります。
ここからは微分・積分の知識が必要なんですね。両辺をで割って、
の極限(つまりバラバラのベンチではなく、100メートルの長いすに自由に座る)を考えると、
これが指数分布の確率密度分布なんです! ここで
としましたが、これは平均間隔です。
平均してメートルに1回ぶつかるとすると(イタイ)、メートル歩くまでにぶつかる確率が上式となります。 ではこの状況下で、1メートルで平均何回人とぶつかるでしょう?答えは、パラメータとした**ポアソン分布**になるのです!(覚えてましたか?)
分布の形状
基本情報
確率
-
Excel での累積分布関数 (c.d.f.) と 確率密度関数 (p.d.f.)の求め方
| A | B | |
|---|---|---|
| 1 | データ | 説明 |
| 2 | 0.5 | 対象となる値 |
| 3 | 8 | 分布のパラメータ Beta の値 |
| 4 | 数式 | 説明(計算結果) |
| 5 | =1-EXP(-A2/A3) | 上のデータに対する累積分布関数の値 |
| 6 | =EXP(-A2/A3)/A3 | 上のデータに対する確率密度関数の値 |
分位点
| A | B | |
|---|---|---|
| 1 | データ | 説明 |
| 2 | 0.5 | この分布の確率 |
| 3 | 1.7 | ��分布のパラメータ Beta の値 |
| 4 | 数式 | 説明(計算結果) |
| 5 | =-A3*LN(1-A2) | 上のデータに対する累積分布関数の逆関数の値 |
分布の特徴
平均 -- 分布の"中心"はどこ? (定義)
- 分布の平均は と与えられます。
標準偏差 -- 分布はどのくらい広がっているか(定義)
- 分布の標準偏差は と与えられます。
歪度 -- 分布はどちらに偏っているか(定義)
- 分布の歪度は です。
尖度 -- 尖っているか丸まっているか (定義)
- 分布の尖度は です。
乱数
-
乱数 x は一様乱数 U に対して次式で生成されます(逆関数法) :
-
Excel での乱数生成法
| A | B | |
|---|---|---|
| 1 | データ | 説明 |
| 2 | 0.5 | 分布のパラメータ Beta の値 |
| 3 | 数式 | 説明(計算結果) |
| 4 | =-A2*LN(1-NTRAND(100)) | 100個の指数乱数を Mersenne Twister アルゴリズムで生成します。 |
メモ: この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A4:A103 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。