メインコンテンツまでスキップ

ベータ分布(Beta distribution)

納期に間に合うか？ベータ分布​

工期見積もり​

ベータ分布が表舞台に現れる数少ない例が、PERT（Program Evaluation and Review Technique）という工期見積もり手法である。

以下のストーリー性あふれる例を見てみよう。​

今回新たなプロジェクトがスタートした。なんとしてでも期限までに完了させたい。
楽観的に考えると1ヵ月後には納品できるという意見もある。 しかし、毎晩布団に潜ると不安が襲って来る。ここはラテンアメリカではないのだ！心配要素は数えればいくらでもある。最悪の場合、納期が遅れて6ヵ月後になる可能性だってあり得る。 プロジェクトメンバーの大半の意見とこれまで実績から、一番可能性のある納期の試算は2ヶ月半と出た。

では納期の期待値はいったいいつと判断すべきなのでしょうか。
PERT では3点見積もりという方法で納期の期待値を算出しています。

納期の期待値 = (楽観値+4×最可能値+悲観値）÷6

この場合では、8.5÷6[ヶ月]。大体1月半くらいになるでしょうか。実はこの算式の正体は、工期の確率分布をベータ分布とした場合の期待値の簡易算式です（簡易式なので実際のベータ分布の期待値とは一致しませんが）。

分布の万能選手​

その利用例の少なさとは裏腹に、この分布は実に優れた特徴を持っています。それは、極めてバラエティーに富んだ分布形状を取ることができることなのです。

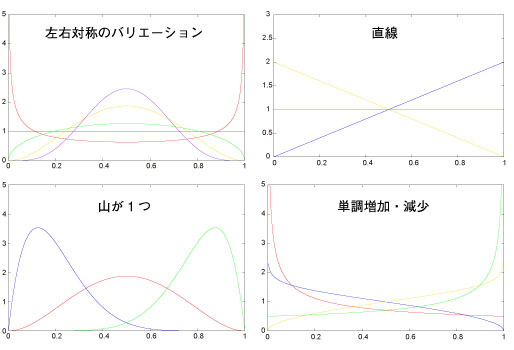
Beta Distributions
このように様々な形状がとれるので、素性不明の分布があれば、適当にパラメータを調整してフィッティングが出来るでしょう。
さあ、では例を見てみましょう。
1棟あたり100戸、全100棟。総戸数10000戸のマンモス団地で、ある商品を売るために100人の大営業部隊を投入することにしました。1人1棟担当し、全戸を回るローラー作戦を実行です。
この商品がこの団地で売れる確率は、平均的な力量をもった営業マンならば p=0.25p=0.25 だったとしましょう。つまり、4件に1件は買ってくれるということ。

  • 驚くべきことに営業マンの力量が全員一定の場合。
    この場合1棟（100戸）あたりで売れる商品の数は p=0.25p=0.25 の成功確率で100回トライする二項分布になるので、xx個売れる確率は、

    f(x)=(100x)(1−0.25)100−x(0.25)xf(x)=\begin{pmatrix}100\\x\end{pmatrix}(1-0.25)^{100-x}(0.25)^{x}

    となります。

  • やっぱり営業マンの力量が一定でない場合。
    入ったばかりの新人営業マンや、この道一筋のカリスマ営業マンなど、100人もいえば様々な力量を持った営業マンがいるでしょう。すると売れる確率は p=0.25p=0.25 ではなく、図のような分布になったとします。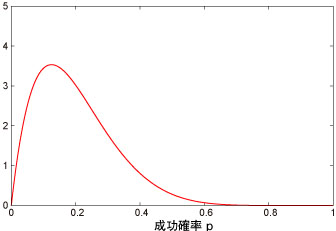

    Probability of Succession
    この分布は何分布なのでしょうか？こんなものにはモデルなどありません。そこでベータ分布の登場なのです。ベータ分布のパラメータを上手に調整して、この分布は B(2,8)B(2,8) に従うとしたとしましょう。 この場合、1棟当たりの売上の分布は、

    f(x)=(100x)(1−p)100−xpxf(x)=\begin{pmatrix}100\\x\end{pmatrix}(1-p)^{100-x}p^{x}

    という二項分布の式で、成功確率 pp 自体がベータ分布に従うという、ベータ二項分布（別名：負の超幾何分布、ポリア=エッゲンベルガー分布）になるのです！

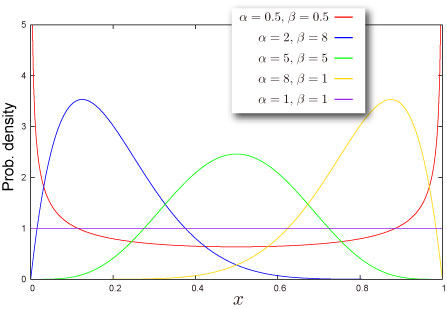
分布の形状​

基本情報​

  • 2つのパラメータ α,β\alpha, \beta が必要です (どうやって求めるの？)

    α>0,β>0\alpha>0,\beta>0

  • 有限区間 0≤x≤10\leq x \leq 1 で定義される連続分布

  • 平均対して対称にも非対称にもなり得ます。

確率​

AB
1データ説明
20.5対象となる値
38分布のパラメータ Alpha の値
42分布のパラメータ Beta の値
5数式説明（計算結果）
6=NTBETADIST(A2,A3,A4,TRUE)上のデータに対する累積分布関数の値
7=NTBETADIST(A2,A3,A4,FALSE)上のデータに対する確率密度関数の値

Triangular distribution

  • 関連 NtRand 関数 : NTBETADIST
  • 第4引数が TRUE の場合、この関数は Excel 関数"BETADIST" と同等です。

分位点​

AB
1データ説明
20.7この分布の確率
31.7分布のパラメータ Alpha の値
40.9分布のパラメータ Beta の値
5数式説明（計算結果）
6=BETAINV(A2,A3,A4)上のデータに対する累積分布関数の逆関数の値

分布の特徴​

平均 -- 分布の"中心"はどこ？ (定義)​

  • 分布の平均 は次式で与えられます。

    αα+β\frac{\alpha}{\alpha+\beta}

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTBETAMEAN(A2,A3)上のデータに対する分布の平均

標準偏差 -- 分布はどのくらい広がっているか（定義）​

  • 分布の分散 は次式で与えられます。

    αβ(α+β)2(α+β+1)\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}

    標準偏差 は 分散の正の平方根です。

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTBETASTDEV(A2,A3)上のデータに対する分布の標準偏差

歪度 -- 分布はどちらに偏っているか(定義)​

  • 分布の歪度 は次式で与えられます。

    2(β−α)α+β+1(α+β+2)αβ\frac{2(\beta-\alpha)\sqrt{\alpha+\beta+1}}{(\alpha+\beta+2)\sqrt{\alpha\beta}}

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTBETASKEW(A2,A3)上のデータに対する分布の歪度

尖度 -- 尖っているか丸まっているか (定義)​

  • 分布の尖度 は次式で与えられます。

    6α3−α2(2β−1)+β2(β+1)−2αβ(β+2)αβ(α+β+2)(α+β+3)6\frac{\alpha^3-\alpha^2(2\beta-1)+\beta^2(\beta+1)-2\alpha\beta(\beta+2)}{\alpha\beta(\alpha+\beta+2)(\alpha+\beta+3)}

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTBETAKURT(A2,A3)上のデータに対する分布の尖度

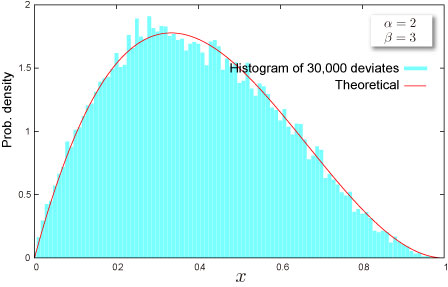
乱数​

  • 乱数生成のアルゴリズムは、

    R. C. H. Cheng, "Generating beta variates with nonintegral shape parameters", Communication of the ACM, 21(1978), pp 317-322

    に従います。

  • Excel での乱数生成法

AB
1データ説明
20.5分布のパラメータ Alpha の値
30.5分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTRANDBETA(100,A2,A3,0)100個のベータ乱数を Mersenne Twister アルゴリズムで生成します。

メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A5:A104 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

関連 NtRand 関数​

  • 既に分布のパラメータをお持ちの場合
  • 分布の平均と標準偏差をお持ちの場合

参照​