メインコンテンツまでスキップ

ワイブル分布(Weibull distribution)

ニータイマーの仕組みワイブル分布​

信頼性工学​

新しく買ったコンピューター。はやる気持ちを抑えて箱から取り出し、早速スイッチを！。。あれ？ウンともスンともいわないぞ。いきなり故障か？
うちのテレビはまだブラウン管。最近突然画面が歪んだり、スイッチが入らなかったり。。。さすがに寿命か？
毎年毎年、冬と夏に1回か2回くらいは風邪をひく。
機械（や人間）はいつ故障するのか？信頼性工学における分析では、 故障率の時間推移は、

  • 時間とともに減少する：初期不良に起因する故障
  • 時間とともに増加する：寿命
  • 時間によらず一定：偶発的な事故

に分類される。グラフにすると

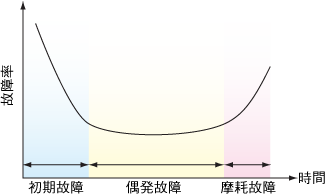
こんな感じ（この形から、バスタブ曲線と呼ばれる）。

故障率をh(t)h(t) として、上記の3つの状況を1つの式で綺麗にモデル可できないかと考えてみる。一番簡単には

h(t)∝tαh(t)\propto t^{\alpha}

としてはどうだろう。α\alphaが正ならば、時間とともに増加する。負ならば減少。そして0ならば時間に依存しなくなる。

故障率がこの式に従うとしたとき、この機械の時刻 t における累積故障率（つまりある時間 t までに故障する確率）がワイブル分布になるのである。

もうひとつ、ワイブル分布が表舞台に現れる理論が極値理論である。

分布の形状​

基本情報​

  • 2つのパラメータ α,β\alpha, \beta が必要です (どうやって求めるの？)。

    α>0,β>0{\alpha}>0,{\beta}>0

  • 半無限区間 x≥0x {\geq} 0 で定義された連続分布です。

  • 平均対して常に非対称です。

確率​

AB
1データ説明
20.5対象となる値
38分布のパラメータ Alpha の値
42分布のパラメータ Beta の値
5数式説明（計算結果）
6=NTWEIBULLDIST(A2,A3,A4,TRUE)上のデータに対する累積分布関数の値
7=NTWEIBULLDIST(A2,A3,A4,FALSE)上のデータに対する確率密度関数の値

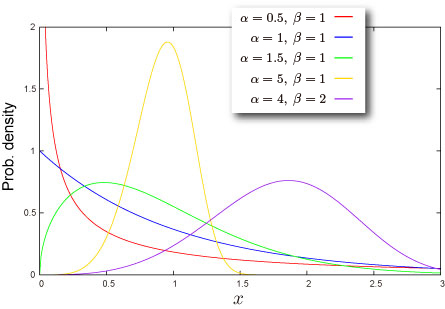
Sample distribution

分位点​

  • 累積確率関数の逆関数

    F−1(P)=β(ln⁡11−P)1/αF^{-1}(P)=\beta\left(\ln\frac{1}{1-P}\right)^{1/\alpha}

  • Excel での分位点の求め方

AB
1データ説明
20.7この分布の確率
31.7分布のパラメータ Alpha の値
40.9分布のパラメータ Beta の値
5数式説明（計算結果）
6=WEIBULLINV(A2,A3,A4)上のデータに対する累積分布関数の逆関数の値

分布の特徴​

平均 -- 分布の"中心"はどこ？ (定義)​

  • 分布の平均 は次式で与えられます。

    βΓ(1+1α)\beta\Gamma\left(1+\frac{1}{\alpha}\right)

    ここで、Γ(⋅)\Gamma(\cdot) は ガンマ関数です。

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTWEIBULLMEAN(A2,A3)上のデータに対する分布の平均

標準偏差 -- 分布はどのくらい広がっているか（定義）​

  • 分布の分散 は次式で与えられます。

    μ′(2)−m2\mu^\prime(2)-m^2

    ここで、

    μ′(r)=βrΓ(1+rα)\mu^\prime(r)=\beta^r\Gamma\left(1+\frac{r}{\alpha}\right)

    、 Γ(⋅)\Gamma(\cdot) は ガンマ関数、mmは分布の平均です。

    標準偏差 は 分散の正の平方根です。

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTWEIBULLSTDEV(A2,A3)上のデータに対する分布の標準偏差

歪度 -- 分布はどちらに偏っているか(定義)​

  • 分布の歪度 は次式で与えられます。

    1σ3[μ′(3)−3mσ2−m3]\frac{1}{\sigma^3}\left[\mu^\prime(3)-3m\sigma^2-m^3\right]

    ここで、

    μ′(r)=βrΓ(1+rα)\mu^\prime(r)=\beta^r\Gamma\left(1+\frac{r}{\alpha}\right)

    、Γ(⋅)\Gamma(\cdot) は ガンマ関数、mmは分布の平均、σ\sigma は 分布の標準偏差です。

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTWEIBULLSKEW(A2,A3)上のデータに対する分布の歪度

尖度 -- 尖っているか丸まっているか (定義)​

  • 分布の尖度 は次式で与えられます。

    μ′(4)−4γ1σ3m−6m2σ2−m4σ4−3\frac{\mu^\prime(4)-4\gamma_1\sigma^3m-6m^2\sigma^2-m^4}{\sigma^4}-3

    ここで、

    μ′(r)=βrΓ(1+rα)\mu^\prime(r)=\beta^r\Gamma\left(1+\frac{r}{\alpha}\right)

    、Γ(⋅)\Gamma(\cdot) は ガンマ関数、mm は分布の平均、σ\sigma は分布の標準偏差、γ1\gamma_1 は分布の歪度です。

  • Excel での計算法

AB
1データ説明
28分布のパラメータ Alpha の値
32分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTWEIBULLKURT(A2,A3)上のデータに対する分布の尖度

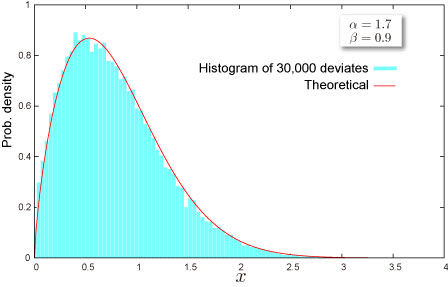
乱数​

  • 乱数 x は一様乱数 U に対して次式で生成されます（逆関数法） :

    x=β(ln⁡11−U)1/αx=\beta\left(\ln\frac{1}{1-U}\right)^{1/\alpha}

  • Excel での乱数生成法

AB
1データ説明
20.5分布のパラメータ Alpha の値
30.5分布のパラメータ Beta の値
4数式説明（計算結果）
5=NTRANDWEIBULL(100,A2,A3,0)100個のワイブル乱数を Mersenne Twister アルゴリズムで生成します。

メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A5:A104 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

関連 NtRand 関数​

参照​