ポアソン分布(Poisson distribution)

馬に蹴られてポアソン分布

概要

恋愛の話じゃありません。馬に蹴られて死んでしまう兵士の数の分布。これこそが歴史上初のポアソン分布の実用例だったのです。驚いたでしょ？
ポアソン分布が現れる例は...

• ある交差点で1時間に起きる事故の件数
• 国道1キロメートル当たりのレストランの数
• この原稿を書いている間に変換間違えをする数

などといったものが考えられます。このようにポアソン分布とは、時間（例えば1時間当たり）、場所（例えば1平方メートル当たり）、距離（例えば1キロメートル当たり）などある一定区間の中で、偶然に起こる事象の数の分布です。
でもこれは一般的には起こる確率の低い事象に対する分布なので、注意したいところです。（ほら、なかなか馬に蹴られて死なないでしょ？）別名「少数の法則」とも呼ばれています（発生件数が多い場合は正規分布に近くなります）。

例えば以下のリアリティー溢れる例

金曜の夕方のオフィス。あと1時間で終業時間、そのあと友達と夕食の約束がある。予約の取りにくいレストランなので、飛び込みの仕事などの残業は絶対にしたくない！ 今のところ今日までの仕事は全て片付けたはず。あとは上司や先輩からメールで突然仕事が降ってこないことを祈るのみ。むむむ、受信箱を開くのが怖い。
今日今までに来たメールは8時間で26通。さて、あと1時間で何通くるんだろう？

ここでポアソン分布が活躍するのです。\

ポアソン分布は「1単位区間あたり平均 $\nu$（ギリシャ文字で"ニュー"）件起きる事象が、$x$件発生する確率」を次式で与えてくれます。

$$f(x)=\frac{\nu^{x}e^{-\nu }}{x!}$$

では今の状況に当てはめてみましょう。知りたいのは、これからの1時間で来るメール数。過去8時間のメールの受信数から1時間当たり平均受信件数は 26÷8=3.25 [通/時間]であることが分かりますね。 したがって1時間に受け取るメール数は $\nu=3.25$のポアソン分布となるのがわかります。

$$f(x)=\frac{3.25^{x}e^{-3.25}}{x!}$$

ここから、例えばメールが3通来る確率は、

$$f(3)=\frac{3.25^{3}e^{-3.25}}{3!}=0.2218$$

つまり大体 22％となります。また1通もメールが来ない（0通のメールが来る）確率は

$$f(0)=\frac{3.25^{0}e^{-3.25}}{0!}=0.039$$

4％程度、つまり96％の確率でメールがやってくることになります。残念ながらこのままサックリとは帰れそうにないみたいですね。

あと1時間...。今までの経験から7通くらいのメールなら1時間でなんとか処理できそう。だったら7通以下のメールが来る確率を計算してみましょう。これは、1通も来ない確率、1通来る確率、2通来る確率...7通来る確率の和になります。

$$f(0)+f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)=0.982$$

つまり、

**「98％の確率で、これからの1時間に受け取るメールは7通以下」**ということ。

98％の確率で定時に帰れる！楽しい金曜の夜になりそうです。

ところで1時間に7通といっても、だいたい5分おきくらいに均等にメールが来るかもしれないし、30分来ないと思ったら一気に連続してメールが来るかもしれないですよね？ 受信したメールと次に来るメールの間隔はどのような分布になっているのでしょうか？実は、それは指数分布になることが分かっているのです。

分布の形状

基本情報

• パラメータ $\nu$ が必要です。

  $$\nu>0$$

  このパラメータは分布の平均です。

• 非負の整数 $x={0,1,2,\cdots}$ で定義される離散分布です。

確率

• 累積分布関数

  $$F(x)=\text{e}^{-\nu}\sum_{i=0}^{x}\frac{\nu^i}{i !}$$

• 確率質量関数

  $$f(x)=\frac{\nu^x\text{e}^{-\nu}}{x !}$$

• Excel での累積分布関数 (c.d.f.) と 確率質量関数 (p.m.f.)の求め方

	A	B
1	データ	説明
2	3	対象となる値
3	5	分布のパラメータ nu の値
4	数式	説明（計算結果）
5	=NTPOISSONDIST(A2,A3,TRUE)	上のデータに対する累積分布関数の値
6	=NTPOISSONDIST(A2,A3,FALSE)	上のデータに対する確率密度関数の値

• 関連 NtRand 関数 : NTPOISSONDIST

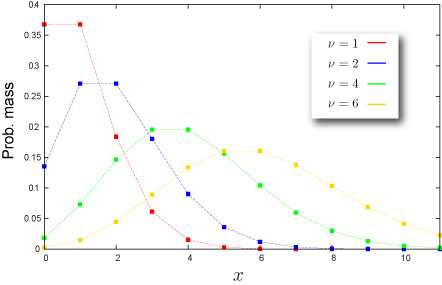
分布の特徴

平均 -- 分布の"中心"はどこ？ (定義)

• 分布の平均は $\nu$ と与えられます。

標準偏差 -- 分布はどのくらい広がっているか（定義）

• 分布の標準偏差は $\nu$ と与えられます。

  標準偏差 は 分散の正の平方根です。

歪度 -- 分布はどちらに偏っているか(定義)

• 分布の歪度 は次式で与えられます。

  $$\frac{1}{\sqrt{\nu}}$$

• Excel での計算法

	A	B
1	データ	説明
2	8	分布のパラメータ nu の値
3	数式	説明（計算結果）
4	=NTPOISSONSKEW(A2)	上のデータに対する分布の平均

• 関連 NtRand 関数 : NTPOISSONSKEW

尖度 -- 尖っているか丸まっているか (定義)

• 分布の尖度 は次式で与えられます。

  $$\frac{1}{\nu}$$

• Excel での計算法

	A	B
1	データ	説明
2	8	分布のパラメータ nu の値
3	数式	説明（計算結果）
4	=NTPOISSONKURT(A2)	上のデータに対する分布の平均

• 関連 NtRand 関数 : NTPOISSONKURT

乱数

Excel での乱数生成法

	A	B
1	データ	説明
2	6	分布のパラメータ nu の値
3	数式	説明（計算結果）
4	=NTRANDPOISSON(100,A2,0)	100個のポアッソン乱数を Mersenne Twister アルゴリズムで生成します。

メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A4:A103 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

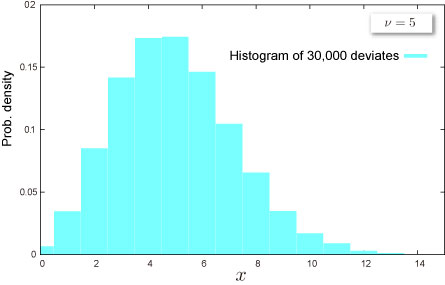
関連 NtRand 関数

• 既に分布のパラメータをお持ちの場合
  • Mersenne Twiseter 法による乱数生成 : NTRANDPOISSON
  • 確率計算 : NTPOISSONDIST
  • 平均計算 : NTPOISSONMEAN
  • 標準偏差計算 : NTPOISSONSTDEV
  • 歪度計算 : NTPOISSONSKEW
  • 尖度計算 : NTPOISSONKURT
  • 上記の各モーメントを一度に計算 : NTPOISSONMOM

参照

• Wolfram Mathworld -- Poisson Distribution
• Wikipedia -- Poisson distribution
• Statistics Online Computational Resource
• Accident : The number of soldiers killed by horse-kicks each year in each corps
• Queuing Theory : Number of phone calls per minuite, number of access to web sever per minuite
• Biology : Number of mutations
• Nuclear physics : the nuclear decay of atoms
• Risk management -- Operational risk